이우의 개발일지
[프로그래머스 / C++] 2024 kakao winter internship 문제 -도넛과 막대 그래프 본문
프로그래머스 도넛과 막대 그래프 문제
문제 설명
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프들이 있습니다. 이 그래프들은 1개 이상의 정점과, 정점들을 연결하는 단방향 간선으로 이루어져 있습니다.
- 크기가 n인 도넛 모양 그래프는 n개의 정점과 n개의 간선이 있습니다. 도넛 모양 그래프의 아무 한 정점에서 출발해 이용한 적 없는 간선을 계속 따라가면 나머지 n-1개의 정점들을 한 번씩 방문한 뒤 원래 출발했던 정점으로 돌아오게 됩니다. 도넛 모양 그래프의 형태는 다음과 같습니다.
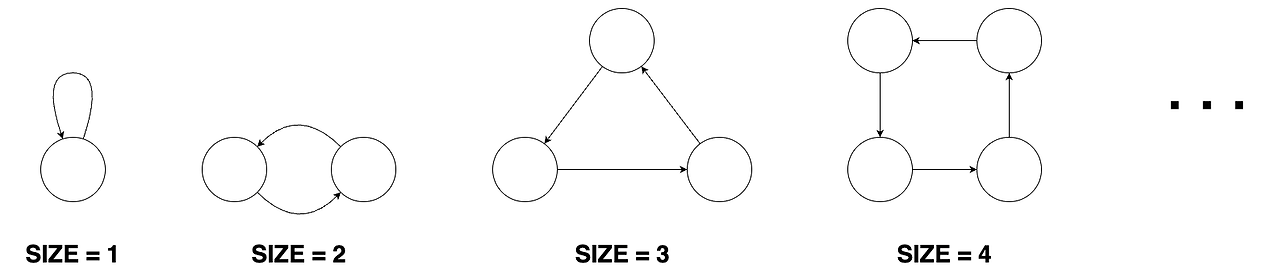
- 크기가 n인 막대 모양 그래프는 n개의 정점과 n-1개의 간선이 있습니다. 막대 모양 그래프는 임의의 한 정점에서 출발해 간선을 계속 따라가면 나머지 n-1개의 정점을 한 번씩 방문하게 되는 정점이 단 하나 존재합니다. 막대 모양 그래프의 형태는 다음과 같습니다.
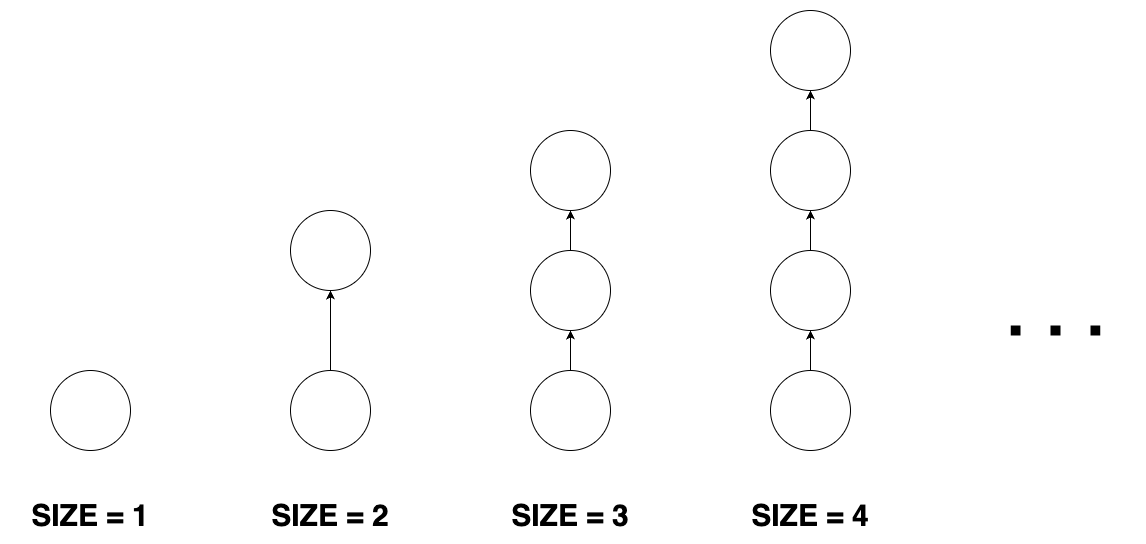
- 크기가 n인 8자 모양 그래프는 2n+1개의 정점과 2n+2개의 간선이 있습니다. 8자 모양 그래프는 크기가 동일한 2개의 도넛 모양 그래프에서 정점을 하나씩 골라 결합시킨 형태의 그래프입니다. 8자 모양 그래프의 형태는 다음과 같습니다.
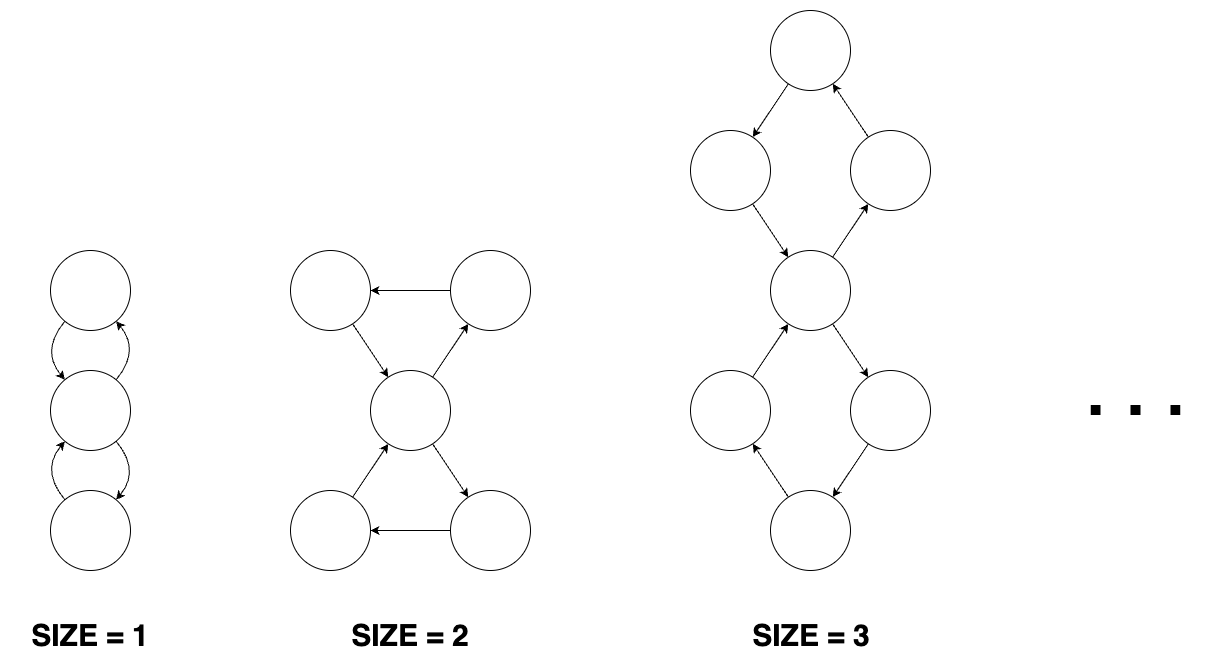
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프가 여러 개 있습니다. 이 그래프들과 무관한 정점을 하나 생성한 뒤, 각 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 임의의 정점 하나로 향하는 간선들을 연결했습니다.
그 후 각 정점에 서로 다른 번호를 매겼습니다.
이때 당신은 그래프의 간선 정보가 주어지면 생성한 정점의 번호와 정점을 생성하기 전 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 구해야 합니다.
그래프의 간선 정보를 담은 2차원 정수 배열 edges가 매개변수로 주어집니다. 이때, 생성한 정점의 번호, 도넛 모양 그래프의 수, 막대 모양 그래프의 수, 8자 모양 그래프의 수를 순서대로 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- 1 ≤ edges의 길이 ≤ 1,000,000
- edges의 원소는 [a,b] 형태이며, a번 정점에서 b번 정점으로 향하는 간선이 있다는 것을 나타냅니다.
- 1 ≤ a, b ≤ 1,000,000
- 문제의 조건에 맞는 그래프가 주어집니다.
- 도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.
도넛과 막대 그래프 풀이
문제 유형은 생소하지만, 천천히 들여다보면 그렇게 어렵지 않은 문제인 것을 알 수 있다.
먼저, 3가지 유형 도넛, 막데, 8자 모양의 그래프 모형의 특징을 파악해야 한다.
- 도넛 모양 : N개의 정점, N개의 간선
- 막대 모양 : N개의 정점, N-1개의 간선
- 8자 모양 : 2N+1개의 정점, 2N+2의 간선
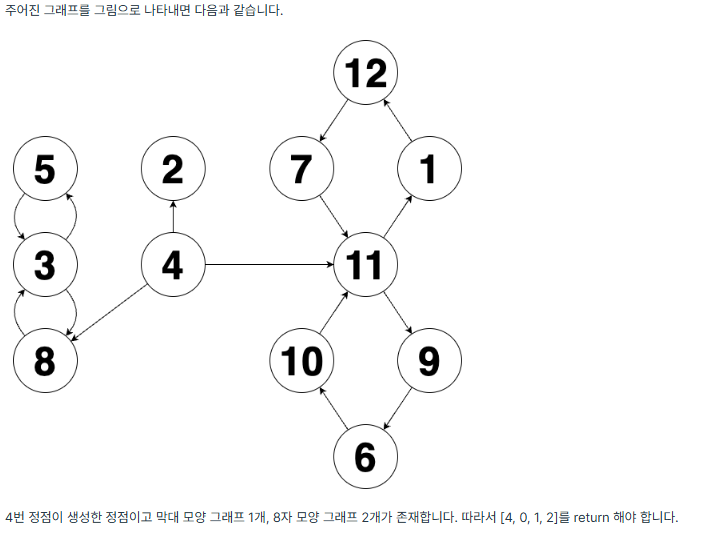
여기서 주의할 점은 생성한 정점을 파악해야한다는 것이다. 위의 그림 예제처럼 4는 생성하는 정점이기 때문에 4번에서 나가는 간선과 정점은 포함하면 안된다.
또한, 여기서 생각해야하는 부분이 있다. 생성한 정점을 선택할 때 vector를 하나씩 파악한다. 이때 한 가지 주요한 특징은 생성한 정점으로 들어가는 간선은 없다는 것이다. 그래서 무턱대고 나가는 간선이 많다고 해서 생성하는 정점이 아니다!
이렇게 생성한 정점을 구했으면, 그 정점을 기준으로 BFS를 돌리면 된다. 각 BFS 가 끝날 때마다 정점과 간선의 개수를 보고 어떤 모양의 그래프인지 파악하여 ++ 해주면 끝이다.
도넛과 막대 그래프 전체 풀이
#include <bits/stdc++.h>
using namespace std;
vector<int> solution(vector<vector<int>> edges) {
// 1. 전체 정점 번호의 최대값 구하기
int maxV = 0;
for (auto &edge : edges) {
maxV = max(maxV, max(edge[0], edge[1]));
}
// 2. 각 정점의 in-degree, out-degree 및 방향 그래프 구성
vector<int> indeg(maxV+1, 0), outdeg(maxV+1, 0);
vector<vector<int>> directed(maxV+1);
for (auto &edge : edges) {
int u = edge[0], v = edge[1];
outdeg[u]++;
indeg[v]++;
directed[u].push_back(v);
}
// 3. extra 정점은 “생성된 정점”이므로,
// (1) 다른 정점에서 들어오는 간선이 없어야 하고 (in-degree == 0)
// (2) 각 컴포넌트로 향하는 간선을 여러 개 가져야 하므로 out-degree가 2 이상이어야 함.
int extra = -1;
for (int i = 1; i <= maxV; i++) {
if(indeg[i] == 0 && outdeg[i] >= 2) {
extra = i;
break;
}
}
// 혹시 위 조건에 맞는 게 없으면, in-degree==0이면서 out-degree > 0인 정점 중 선택
if(extra == -1) {
for (int i = 1; i <= maxV; i++) {
if(indeg[i]==0 && outdeg[i]>0) {
extra = i;
break;
}
}
}
// 4. extra 정점과 연결된 각 컴포넌트(원래의 도넛/막대/8자 그래프)는
// extra 정점의 간선으로 들어간 정점들이 entry point가 됨.
// 단, 막대형은 방향 그래프상 entry point가 전체를 도달하지 못할 수 있으므로
// “방향 무시 연결(undirected connectivity)”로 전체 컴포넌트를 구합니다.
// extra 정점은 컴포넌트에 포함되지 않으므로 무시합니다.
// undirected 그래프 구성 (extra 정점과 관련된 간선은 제외)
vector<vector<int>> undirected(maxV+1);
for (auto &edge : edges) {
int u = edge[0], v = edge[1];
if(u == extra || v == extra) continue;
undirected[u].push_back(v);
undirected[v].push_back(u);
}
// 컴포넌트 탐색을 위한 방문 배열 (undirected 기준)
vector<bool> compVisited(maxV+1, false);
// extra 정점에서 뻗은 간선의 도착 정점들을 모읍니다.
vector<int> extraNeighbors = directed[extra];
sort(extraNeighbors.begin(), extraNeighbors.end());
extraNeighbors.erase(unique(extraNeighbors.begin(), extraNeighbors.end()), extraNeighbors.end());
// 각 컴포넌트 별 그래프 분류를 위한 카운터
int donut = 0, bar = 0, eight = 0;
// 각 컴포넌트에서 “정점 수”와 “그 컴포넌트 내에서 존재하는 원래 간선의 수”를 셉니다.
// 분류 조건:
// • 도넛 그래프: 정점 수 == 간선 수
// • 막대 그래프: 정점 수 == 간선 수 + 1
// • 8자 그래프: 간선 수 == 정점 수 + 1
vector<int> compMark(maxV+1, 0); // 컴포넌트 소속 여부를 체크 (멤버십 마킹)
for (int nb : extraNeighbors) {
if(nb < 1 || nb > maxV) continue;
if(compVisited[nb]) continue;
// undirected DFS/BFS로 이 컴포넌트의 모든 정점을 수집
vector<int> compVertices;
queue<int> q;
q.push(nb);
compVisited[nb] = true;
while(!q.empty()){
int cur = q.front(); q.pop();
compVertices.push_back(cur);
for (int nxt : undirected[cur]) {
if(!compVisited[nxt]) {
compVisited[nxt] = true;
q.push(nxt);
}
}
}
// 컴포넌트 내 정점 집합에 대해 멤버십 표시
for (int v : compVertices) {
compMark[v] = 1;
}
// 원래 주어진 방향 그래프에서, 컴포넌트 내에 있는 간선만 세기
int vertexCount = compVertices.size();
int edgeCount = 0;
for (int v : compVertices) {
// directed[v]에 있는 간선 중
for (int w : directed[v]) {
if(w == extra) continue; // extra 정점은 제외
if(compMark[w] == 1) edgeCount++;
}
}
// 컴포넌트 마킹 초기화
for (int v : compVertices) {
compMark[v] = 0;
}
// 분류 조건에 따라 카운트 증가
if(vertexCount == edgeCount) {
donut++;
} else if(vertexCount == edgeCount + 1) {
bar++;
} else if(vertexCount + 1 == edgeCount) {
eight++;
}
}
vector<int> answer;
answer.push_back(extra);
answer.push_back(donut);
answer.push_back(bar);
answer.push_back(eight);
return answer;
}
'Coding' 카테고리의 다른 글
| [백준 / C++ ] 15683번 감시 /시뮬레이션 문제 (0) | 2025.04.01 |
|---|---|
| [프로그래머스 / C++] 혼자 놀기의 달인 Lv.1 (0) | 2025.02.18 |
| [프로그래머스 / C++] Lv. 2 요격시스템 문제 풀이 및 코드 (0) | 2025.02.06 |
| [백준 / C++] 13549 숨박꼭질 (3) - (1) (0) | 2025.01.23 |
| [백준 / C++] 11404 플로이드 - (1) '플로이드-워셜 알고리즘에 대해' (0) | 2025.01.22 |




